「Algorithm」01 基础算法
- 排序
- 二分
- 高精度
- 前缀和与差分
- 位运算
- 离散化
- 区间合并
消除同步
- ios::sync_with_stdio(false);//让cin和标准输入输出不同步,提高cin的读取速度,不能再使用scanf和printf了。
- scanf/getchar和cin不要一起用,printf/puts/putchar和cout不要一起用。
- 可以使用freopen
还可以加上 cin.tie(0) 来解除c++运行库层面的对数据传输的绑定。
排序
1. 快速排序
基于分治。
- 确定一个分界点,比如(以1开始),取q[1],q[(1+r)/2] ,q[r], 随机为x
- 调整区间,小于等于x的在左边,大于等于x的在右边。等于x的可以在左边也可以在右边,也可以在边界上,不稳定。
- 递归处理左右两段。
方法一:
- 开两个额外的数组,a[],b[]
- 扫描q数组,如果q[i] ≤ x,存入a,如果q[i]>x,存入b。
- 然后将a数组的数存入q,b数组的数存入q。
方法二:
- i和j指针,i指向初始,j指向末尾。然后i向右走,直到遇到一个大于x的数。j向左走,直到遇到一个小于等于x的数。然后交换,直到 j ≤ i.
模板:
#include <iostream> using namespace std; const int N = 1e6 + 10; int n; int q[N]; void quick_sort(int q[], int l, int r) { if (l >= r) return; int x = q[(l+r) >> 1], i = l - 1, j = r + 1; while( i < j){ do i ++ ; while (q[i] < x); do j -- ; while (q[j] > x); if (i < j ) swap(q[i],q[j]); } //j可能比i小,也可能等于i。 quick_sort(q, l, j); //也可以换成 l, i -1 quick_sort(q, j + 1, r); //换成 i, r //后来说明不能换成i,因为也是会出现死循环问题。 //遇到这种情况,就考虑0,1。 //用j的话,x不能取右边界,(j可以取q[l]、q[(l+r)/2]) //j不能取 q[r]、q[(l+r+1)/2] //用i的话,x不能取左边界。 (i可以取q[r]、q[(l+r+1)/2]) //i不能取 q[l]、q[(l+r)/2] } //当下面换成i,r时,不能取x=q[l],因为会出现死循环的问题。比如排序1,2 //i最终为0,j也是0,这样使用quick_sort()会死循环。 //同理,如果取j+1,r,不能取右边界。 int main(){ scanf("%d",&n); for(int i = 0; i < n; i ++ ) scanf("%d",&q[i]); quick_sort(q,0,n-1); for(int i = 0; i < n; i ++ ) printf("%d ",q[i]); return 0; } 排序的话,可以使用 #include<algorithm> sort(q, q+n);
2.归并排序
类似快排,也是分治。
- 以中间点为分界点。
- 递归排序左边和右边。
- 归并左右两个有序的数组为1个有序的数组。
- 对两个数组,取两个指针指向数组的左端点。然后比较他们的值,取较小者,然后移动指针,接着继续比较,直到一个指针到头,然后将另一个数组的剩余值取走。
- 当指针指向的值相同时,取左边数组的值,保持稳定,这说明归并排序是稳定的。快排是不稳定的。而让快排稳定的话,可以用pair。
为什么归并排序是O(nlogn),怎么分析?
归并排序总共有logn层,每层都是O(n),所以是O(nlogn)

#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int n;
int q[N], tmp[N];
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int mid = (l + r) >> 1; //+优先级比>>大,可以不加括号
merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while ( i <= mid) tmp[k++] = q[i++];
while ( j <= r) tmp[k++] = q[j++];
for ( i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
int main(){
scanf("%d",&n);
for(int i = 0; i < n; i ++ ) scanf("%d",&q[i]);
merge_sort(q, 0, n-1);
for(int i = 0; i < n; i ++ ) printf("%d ",q[i]);
return 0;
}
二分
1. 整数二分
模板:
// 区间[l,r]被划分为[l,mid]与[mid + 1,r]时用
int bsearch_1(int l, int r) {
while( l < r)
{
int mid = l + r >> 1;
if (check(mid)) r= mid; //check判断mid是否满足性质
else l = mid + 1;
}
return l;
}
//区间[l,r]被划分成[l, mid - 1]和[mid, r]时使用。
int bsearch_2(int l, int r){
while(l < r)
{
int mid = l + r + 1 >> 1;
if(check(mid)) l = mid;
else r = mid -1;
}
return l;
}
- 二分的本质:寻找区间的边界。边界的左边满足某种性质,边界的右边满足另一种性质。

- mid = (l+r+1)/2 找红色的边界点,检测中间值是否满足check。
- check检查是否满足红色。
- if mid满足check,那么需要向右找,那么 l = mid; [mid, r]
- if mid不满足check,那么需要向左找,那么r = mid -1:[l , mid - 1]
- mid = (l + r)/ 2寻找绿色的边界点。check检测是否满足绿色。
- if mid 满足 check, 那么需要向左找,那么 r = mid; [l , mid]
- if mid 不满足 check, 那么需要向右找,那么 l = mid + 1; [mid + 1, r]
为什么第一个需要mid = (l + r + 1)/2 ,因为如果r = l + 1,如果不加一,那么mid = l,区间的更新为:[l,r] 和[l,l],陷入了死循环。
所以总的来说,我们如何使用上面两个?
1,2,2,3,3,4。
找3的起始坐标和终止坐标。
//https://www.acwing.com/problem/content/791/
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n,m;
int q[N];
int main(){
scanf("%d%d", &n, &m);
for(int i = 0; i < n; i++ ) scanf("%d", &q[i]);
while(m--){
int x;
scanf("%d", &x);
int l = 0, r = n -1;
while ( l < r)
{
int mid = l + r >> 1;
if (q[mid] >= x){ //找起始坐标
r = mid;
} else
l = mid + 1;
}
// l == r
if (q[l] != x) cout << "-1 -1" << endl;
else
{
cout << l << " ";
int l = 0, r = n - 1;
while (l < r){
int mid = (l + r + 1) >> 1;
if (q[mid] <= x) l = mid; // l =mid,需要 l+r+1 >> 1
else r = mid - 1;
}
cout << l << endl;
}
}
return 0;
}
2. 浮点数二分
#include<iostream>
using namespace std;
int main(){
double x;
cin >> x;
double l = 0, r= x;
while( r - l > 1e-6){ //1e8
double mid = (l+r)/2;
if (mid * mid >= x)
r = mid;
else l = mid;
}
/*
迭代100次;
for (int i = 0; i < 100; i++){
double mid = (l+r)/2;
if (mid * mid >= x) r = mid;
else l = mid;
}
*/
printf("%lf\n", l);
return 0;
}
//保留几位小数,增加2有效位。保留2位,1e-4
三次方根:
#include<iostream>
#include<cmath>
using namespace std;
int main(){
double x;
cin >> x;
double l = -1000, r= 1000;
while( r - l > 1e-8){
double mid = (l+r)/2;
if (mid * mid *mid >= x)
r = mid;
else l = mid;
}
printf("%lf\n", l);
return 0;
}
牛顿迭代法求平方根:a 是待求平方根的数
$$x = \frac{x^2_0+a}{2x_0}$$
如何通俗易懂地讲解牛顿迭代法求开方?数值分析? - 杨华的回答 - 知乎 https://www.zhihu.com/question/20690553/answer/15864267
高精度
只有C++需要关注。Python默认数是无限大,Java有大整数BigInteger和BigDecimal。
- A + B
- A - B
- A * a len(A) ≤ 10^6 a ≤ 10^9
- A / a 求商和余数
存储方法:比如 123456789
- 给一个数组a[9],那么a[0] = 9,a[1] = 8,……a[8] = 1,数组的低位存数字的低位。
加法:
#include<iostream>
#include<vector>
#include<string>
using namespace std;
const int N = 1e6 + 10;
vector<int> add(vector<int> &A, vector<int>&B){
vector<int> C;
int t = 0; //进位
for(int i = 0; i < A.size() || i < B.size(); i ++){
if (i < A.size()) t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if(t) C.push_back(t);
return C;
}
/*
vector<int> add(vector<int> &A, vector<int>&B){
vector<int> C;
if (A.size() < B.size()) return add(B,A);
int t = 0; //进位
for(int i = 0; i < A.size(); i ++){
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if(t) C.push_back(t);
return C;
}
*/
int main(){
string a,b;
vector<int> A,B;
cin >> a >> b;
for (int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - '0');
auto C = add(A,B);
for (int i = C.size() - 1; i >= 0; i --) printf("%d",C[i]);
return 0;
}
如果每一个存放不止一位数字:
#include <iostream>
#include <vector>
using namespace std;
const int base = 1000000000;
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % base);
t /= base;
}
if (t) C.push_back(t);
return C;
}
int main()
{
string a, b;
vector<int> A, B;
cin >> a >> b;
for (int i = a.size() - 1, s = 0, j = 0, t = 1; i >= 0; i -- )
{
s += (a[i] - '0') * t;
j ++, t *= 10;
if (j == 9 || i == 0)
{
A.push_back(s);
s = j = 0;
t = 1;
}
}
for (int i = b.size() - 1, s = 0, j = 0, t = 1; i >= 0; i -- )
{
s += (b[i] - '0') * t;
j ++, t *= 10;
if (j == 9 || i == 0)
{
B.push_back(s);
s = j = 0;
t = 1;
}
}
auto C = add(A, B);
cout << C.back();
for (int i = C.size() - 2; i >= 0; i -- ) printf("%09d", C[i]);
cout << endl;
return 0;
}
作者:yxc
链接:https://www.acwing.com/activity/content/code/content/39792/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
减法:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
const int N = 1e5 + 10;
bool cmp(vector<int> &A, vector<int>&B) {
if (A.size() != B.size()) return A.size() > B.size();
for(int i = A.size() - 1 ; i >= 0; i--)
if(A[i] != B[i])
return A[i] > B[i];
return true;
}
vector<int> sub(vector<int>&A, vector<int>&B){
vector<int> C;
for (int i = 0, t =0; i < A.size(); ++ i){
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
//数学,当t小于0,就可以+10,而如果t >=0, 就无影响;
if ( t < 0) t = 1; //有借位
else t = 0;
}
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main(){
string a,b;
vector<int> A,B;
cin >> a >> b;
for(int i = a.size() - 1; i >= 0; -- i) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; -- i) B.push_back(b[i] - '0');
if (cmp(A,B)) {
auto C = sub(A,B);
for (int i = C.size() - 1; i >= 0; -- i) printf("%d", C[i]);
} else {
auto C = sub(B,A);
printf("-");
for (int i = C.size() - 1; i >= 0; -- i) printf("%d", C[i]);
}
return 0;
}
乘法:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
const int N = 1e5 + 10;
vector<int> mul(vector<int>&A, int b){
vector<int> C;
int t = 0;
for(int i = 0; i < A.size() || t; ++ i) {
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main(){
string a;
int b;
vector<int> A;
cin >> a >> b;
for(int i = a.size() - 1; i >= 0; -- i) A.push_back(a[i] - '0');
auto C = mul(A,b);
for (int i = C.size() - 1; i >= 0; -- i) printf("%d", C[i]);
return 0;
}
除法:
#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> div(vector<int> &A, int b, int &r) {
vector<int> C;
r = 0;
for(int i = A.size() - 1; i >= 0; -- i) {
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main(){
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; -- i) A.push_back(a[i] - '0');
int r = 0;
auto C = div(A, b, r);
for(int i = C.size() - 1; i >= 0; -- i) printf("%d", C[i]);
cout << endl << r << endl;
return 0;
}
前缀和 与 差分
前缀和与差分是逆运算。
前缀和:
- 一个长度为n的数组
- 然后前缀和数组,Si = 前i个数的和(从a1、a2到ai)。
- 定义$S_0 = 0$;
问题是如何求Si,求前i个和即可。
!作用:求一段数字的和。比如求[l, r],那么就是求
$$S_r - S_{l-1}$$
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N], s[N];
int main(){
//ios::sync_with_stdio(false);//让cin和标准输入输出不同步,提高cin的读取速度,不能再使用scanf和printf了。
//可以,但是scanf/getchar和cin不要一起用,printf/puts/putchar和cout不要一起用。
//可以使用freopen。
cin >> n >> m;
for (int i = 1; i <= n; ++ i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++ i) s[i] = s[i - 1] + a[i];
while(m --)
{
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",s[r] - s[l - 1]);
}
return 0;
}
二维前缀和
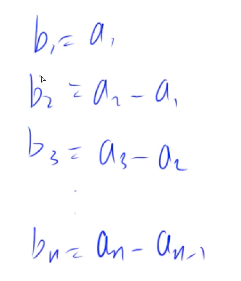
从$(x_1,y_1)\ to \ (x_2,y_2)$,的区域的面积。那么就是:
$$S_{x_2y_2}-S_{x_2(y_1-1)}-S_{(x_1-1)y_2}+S_{(x_1-1)(y_1-1)}$$
#include<iostream>
using namespace std;
int n, m, q;
const int N = 1e3 + 10;
int a[N][N], s[N][N];
int main(){
cin >> n >> m >> q;
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= m; ++ j){
scanf("%d", &a[i][j]);
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
while(q --){
int x1,y1,x2,y2;
scanf("%d%d%d%d", &x1,&y1,&x2,&y2);
printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);
}
return 0;
}
差分
a数组是b数组的前缀和,b数组是a的差分。
对于a1, a2, a3……an
构造 b1, b2, b3, bn
使得 aj = b1 + b2 + …… + bj
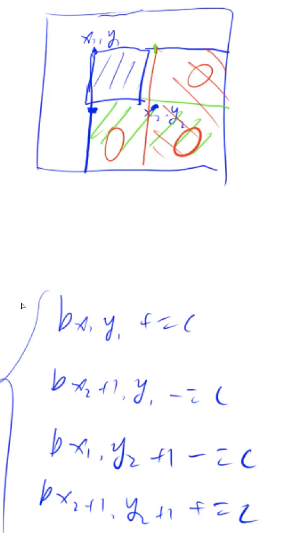
用处:a和b数组在O(n)时间可以相互转化。
让al到ar,[l, r]的数都加上c,用差分只要O(1)。只要让$b_l+c$,然后让 $b_{r+1}-c$
可以假定a数组和b数组全是零,只要看插入操作,即在[1, 1]的数都加上a1, [2,2]的数都加上a2
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N], b[N];
void insert(int l, int r, int c)
{
b[l] += c;
b[r + 1] -= c;
}
int main(){
cin >> n >> m;
for (int i = 1; i <= n; ++ i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++ i) insert(i, i, a[i]);
while(m --) {
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
insert(l, r, c);
}
for (int i = 1; i <= n; ++ i) {
b[i] += b[i-1]; //求前缀和
printf("%d ", b[i]);
}
return 0;
}
差分矩阵

初始化时,也是可以相当于在(i, j)和(i, j)之间增加$a_{i,j}$
b数组是a数组的差分,a数组是b数组的前缀和。
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2+1] -=c;
b[x2+1][y2+1] +=c;
}
int main(){
cin >> n >> m >> q;
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= m; ++ j)
scanf("%d",&a[i][j]);
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= m; ++ j)
insert(i,j,i,j,a[i][j]);
while(q --) {
int x1,y1,x2,y2,c;
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
insert(x1, y1, x2, y2, c);
}
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= m; ++ j){
b[i][j] += b[i -1][j] + b[i][j -1] - b[i- 1][j-1];
printf("%d ", b[i][j]);
}
puts("");
}
return 0;
}
双指针算法
包括归并排序

for(int i = 0, j = 0; i < n; ++ i){
while( j < i && check(i, j)) ++ j;
//具体逻辑
}
核心思想:把O(n^2)两重循环 变成 O(n).
举个例子,输入一个句子,输出每个单词:
#include<iostream>
#include<cstring>
using namespace std;
int main() {
char str[1000];
cin.getline(str, 1000);
int n = strlen(str);
for (int i = 0; i < n; ++ i)
{
int j = i;
while( j < n && str[j] !=' ') ++ j;
for (int k = i; k < j; k ++) cout << str[k];
cout << endl;
i = j;
}
return 0;
}
799. 最长连续不重复子序列
check检验是否有重复元素

//数据很大时可以用hash table来做
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N], s[N];
int main() {
cin >> n;
for (int i = 0; i < n; ++ i )
scanf("%d",&a[i]);
int res = 0;
for (int i = 0, j = 0; i < n; ++ i )
{
++ s[a[i]];
while (j <= i && s[a[i]] > 1) {
-- s[a[j]];
++ j;
}
res = max(res, i - j + 1);
}
cout << res;
return 0;
}
位运算
第k位的值
- n的二进制表示中,第k位是几?个位是第零位。
- 先把第k位移到最后一位, n » k
- 再看个位是几。x & 1.
- 即 (n » k) & 1,»运算符的优先级大于 &,可以不加括号。
lowbit操作。
可以用来统计x中的1的数量。
lowbit(x),返回x的最后一位的1。
Lowbit( 1010) ——> 得到最后一个1。

-x = ~x + 1。 补码表示。
那么 x & -x = x & ( ~x + 1)
#include<iostream>
using namespace std;
int lowbit(int x)
{
return x & -x;
}
int main (){
int n;
cin >> n;
while(n--){
int x;
cin >> x;
int res = 0;
while(x) x -= lowbit(x), ++ res;
cout << res << " ";
}
return 0;
}
一个数 -x 的:
原码:最高位取1.
反码:各位取反
补码:各位取反,加一。

离散化
整数的离散化:
值域为$0-{10}^9$,个数有$10^5$。映射到0-n
比如a[]: 1, 3, 100, 2000, 500000. 将它们映射到0,1,2,3,4,
注意:
- a[]中可能有重复的元素,需要去重
- 如何算出a[i] 离散化后的值是多少?二分。

unique是将alls数组进行去重,将重复元素放在末尾,返回值是一个迭代器,指向非重复元素的最后一个,然后在删除这些元素就好。
找到第一个≥ x的位置, 这个是边界问题。
返回r+1是映射到1,2,……n
Unique
如何实现Unique函数?
比如1 1 2 2 2 3 4 5 5 5 6
vector<int>::iterator unique(vector<int> &a)
{
int j = 0;
for(int i = 0; i < a.size(); ++ i )
{
if (!i || a[i] != a[i-1])
a[j++] = a[i]
}
return a.begin() + j;
}
区间和:
如果数据比较小,就是前缀和和差分的问题。但是这个问题的数据量比较大,而且有负数。
这个问题,是插入的数量比较小。虽然跨度有10亿个,但是查询和插入的数量都是十万不到。所以需要离散化。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 300010;
int n,m;
int a[N], s[N];
vector<int> alls;
vector<PII> add, query;
int find(int x)
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
int main() {
cin >> n >> m;
for(int i = 0; i < n; ++ i )
{
int x, c;
cin >> x >> c;
add.push_back({x,c});
alls.push_back(x);
}
for(int i = 0; i < m; ++ i)
{
int l, r;
cin >> l >> r;
query.push_back(make_pair(l,r));
alls.push_back(l);
alls.push_back(r);
}
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
for(auto item : add)
{
int x = find(item.first);
a[x] += item.second;
}
for (int i = 1; i <= alls.size(); ++ i) s[i] = s[i - 1] + a[i];
for (auto item: query)
{
int l = find(item.first), r = find(item.second);
cout << s[r] - s[l - 1] << endl;
}
return 0;
}
区间合并
把有重叠点的区间合并

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 200010;
typedef pair<int, int> PII;
vector<PII> segs;
int n;
void merge(vector<PII> & segs)
{
vector<PII> res;
sort(segs.begin(), segs.end()); //先排first,再排second
int st = -2e9, ed = -2e9; //st = start, ed = end
for(auto seg : segs)
{
if (ed < seg.first)
{
if (st != -2e9) res.push_back({st, ed});
st = seg.first, ed = seg.second;
}
else
{
ed = max(ed, seg.second);
}
}
if (st != -2e9) res.push_back({st, ed});
segs = res;
}
int main()
{
cin >> n;
for (int i = 0; i < n; ++ i)
{
int l, r;
cin >> l >> r;
segs.push_back({l, r});
}
merge(segs);
cout << segs.size() << endl;
return 0;
}